双纽线极坐标方程推导(设计师的偏爱----贝努里双纽线)
——奇妙有趣的几何之曲线曲面系列
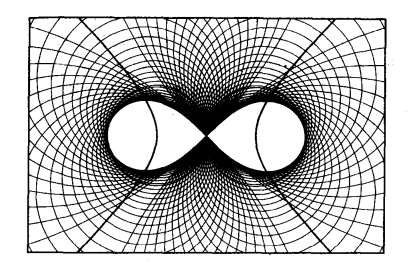
伯努利双纽线,也称双纽线。1694年雅各布·伯努利将其作为椭圆的一种类比来处理。椭圆是由到两个定点距离之和为定值的点的轨迹。而到两定点距离之乘积为定值的点的轨迹是卡西尼卵形线。当此轨迹经过两定点的中点时,便为伯努利双纽线。伯努利将这种曲线称为lemniscate,为拉丁文中“悬挂的丝带”之意。

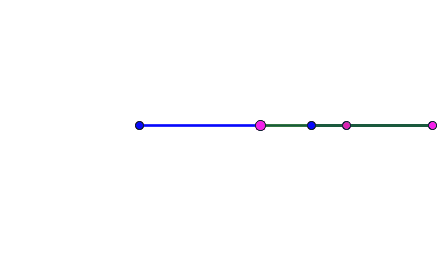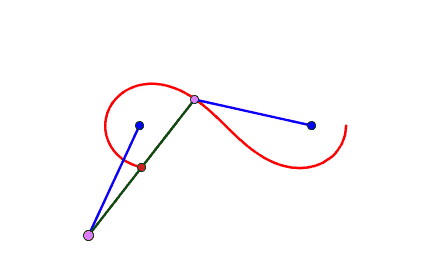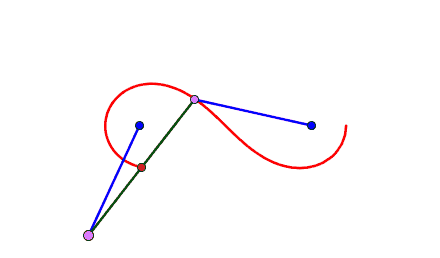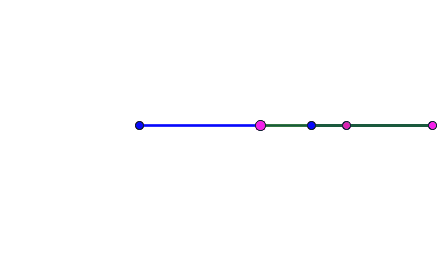
为把双纽线作为包络画出,从等轴双曲线出发,以双曲线上的点为圆心,经过双曲线的中心画圆,这些圆的包络就是双纽线双纽线是双曲线关于其中心的反演.选一个常数k,过等轴双曲线的中心O画一条直线,交双曲线于点X.在OX上求点Y,使OX×OY=k^2,则点Y的轨迹就是双纽线。
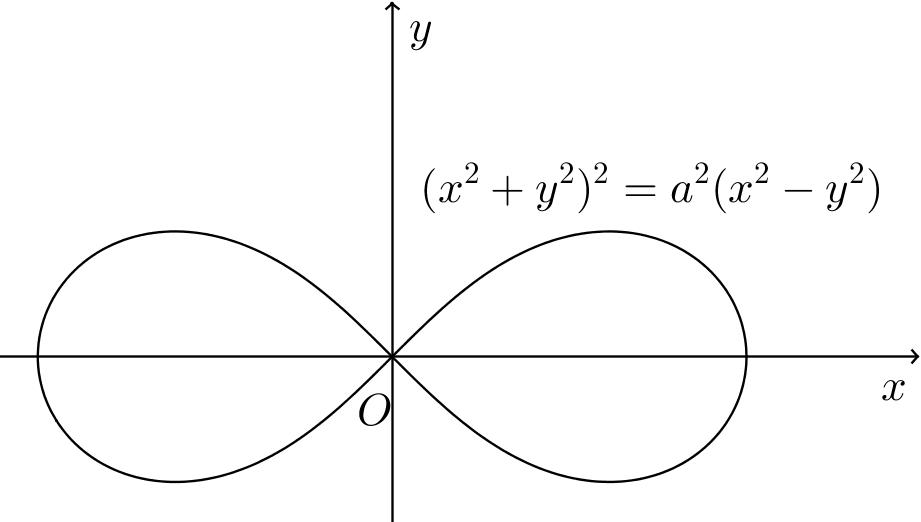
在数学中,对于长度为2a的定线段 ,双纽线的方程和性质如图.


双纽线的极坐标方程是r=a^2cos2θ.双线是卡西尼卵形线的特殊情况.
双组线可用一个很简单的联合器作出.两个定点之间的距离等于中间一节的杆长,另两节的长是它的长的√2倍中间节杆的中心画出的轨迹就是双纽线。
伯努利双纽线在科技和轻工业领域也得到了广泛应用,伯努利还将伯努利双纽线应用于赌博术中。 常见应用如
(1)在纺织中的应用: 伯努利双纽线在纺织中作为花纹得到广泛应用, 用双纽线编织的布料外形美观,结构紧密,具有重复性和渐变性。
(2)在增压器中的应用: 伯努利双纽线无撞击双进气拓宽流量增压器在工业中得到广泛应用。
(3)在赌博术中的应用:在雅各布·伯努利的《猜度术》一书中,将伯努利双纽线广泛应用到赌博术中。
双纽线函数图形既体现了数学的美又具有艺术的美。通常作为艺术设计的几何元素。双纽线函数图形轮廓像阿拉伯数字中的“8”,在中国8更丰富的意思。通过双纽线的外延和内涵,在不对其变形的基础上,对双纽线函数图形进行可用图式的概括,在此基础上可以创作出许多优秀的艺术作品 。

双纽线函数图形在纺织中的图式有
(1)重复型
对双纽线函数图形进行重复构图,可在纺织品中用作花边或底纹进行修饰,从而增加趣味和美感。
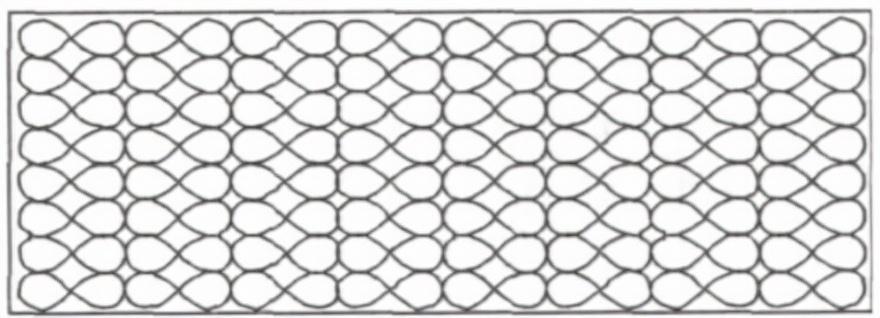
(2)渐次型
运用双纽线函数图形进行渐变构图,表现出同方向的递增和递减,具有一定的规律性,视觉上容易给人秩序的美感。能在众多纺织品中突显。
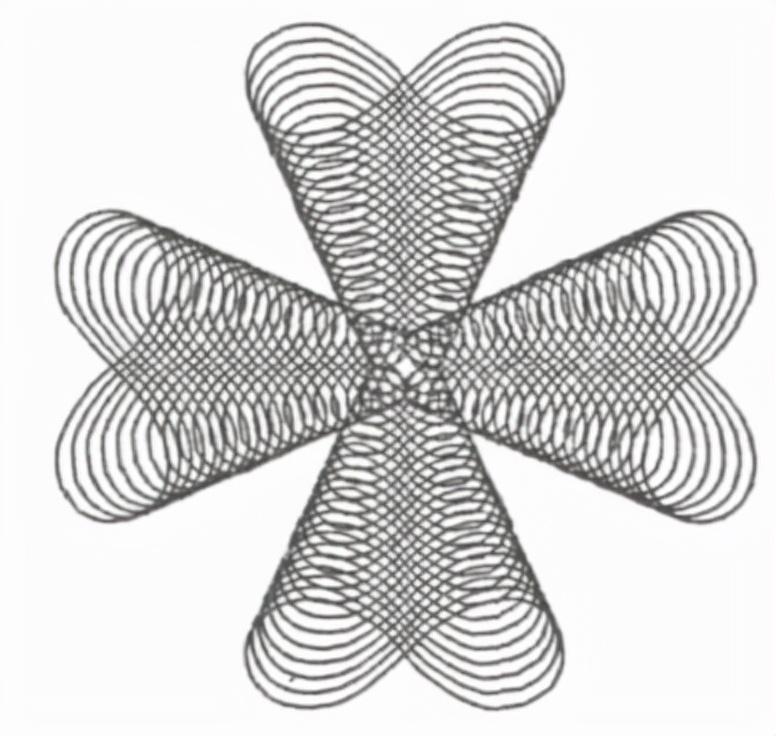
(3)对称型
双纽线函数图形本身就具有对称的美感,在其本身就可做出对称的多种形式,适用于纺织品中。
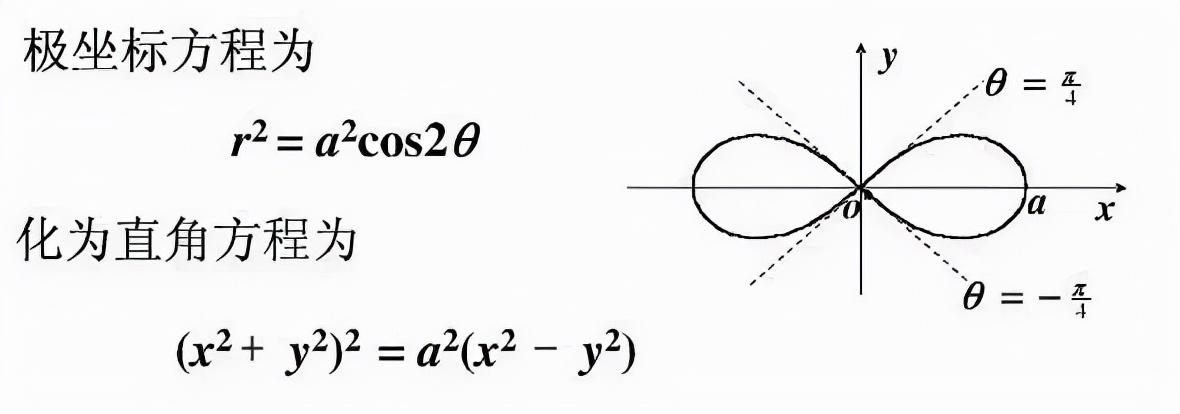
(4)重叠型
通过对双纽线函数图形进行旋转式重叠,构成一个花式图形,在纺织品中能增加其视觉效果。
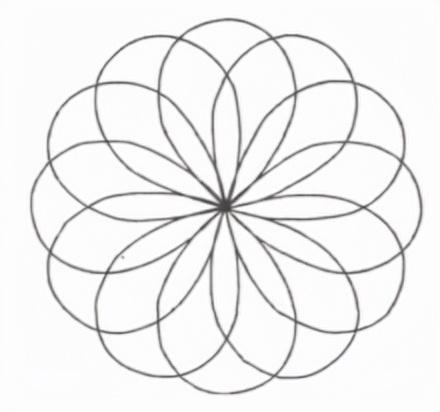
(5)发射型
由双纽线函数图形组合成发射型图式,是一种特殊的重复,是双纽线函数图形环绕一个或多个中心点向外散开或向内集中。